If you’ve spent any time looking at online NLP resources, you’ve probably run into spelling correctors. Writing a simple but reasonably accurate and powerful spelling corrector can be done with very few lines of code. I found this sample program by Peter Norvig (first written in 2006) that does it in about 30 lines. As an exercise, I decided to port it over to Estonian. If you want to do something similar, here’s what you’ll need to do.
First: You need some text!
Norvig’s program begins by processing a text file—specifically, it extracts tokens based on a very simple regular expression.
import re
from collections import Counter
def words(text): return re.findall(r'\w+', text.lower())
WORDS = Counter(words(open('big.txt').read()))The program builds its dictionary of known “words” by parsing a text file—big.txt—and counting all the “words” it finds in the text file, where “word” for the program means any continuous string of one or more letters, digits, and the underscore _ (r'\w+'). The idea is that the program can provide spelling corrections if it is exposed to a large number of correct spellings of a variety of words. Norvig’s ran his original program on just over 1 million words, which resulted in a dictionary of about 30,000 unique words.
To build your own text file, the easiest route is to use existing corpora, if available. For Estonian, there are many freely available corpora. In fact, Sven Laur and colleagues built clear workflows for downloading and processing these corpora in Python (estnltk). I decided to use the Estonian Reference Corpus. I excluded the chatrooms part of the corpus (because it was full of spelling errors), but I still ended up with just north of 3.5 million unique words in a corpus of over 200 million total words.
Measuring string similarity through edit distance
Norvig takes care to explain how the program works both mechanically (i.e., the code) and theoretically (i.e., probability theory). I want to highlight one piece of that: edit distance. Edit distance is a means to measure similarity between two strings based on how many changes (e.g., deletions, additions, transpositions, …) must be made to string1 in order to yield string2.
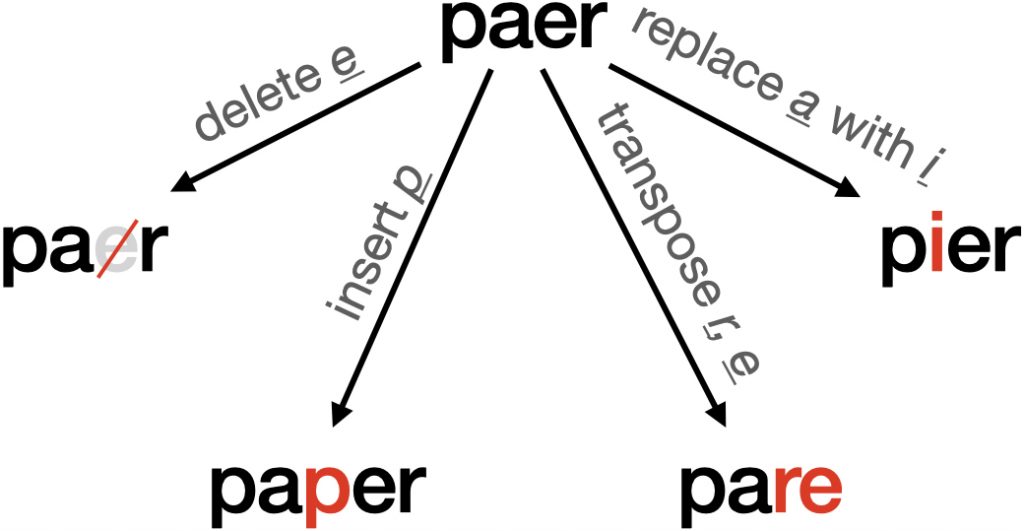
The spelling corrector utilizes edit distance to find suitable corrections in the following way. Given a test string, …
- If the string matches a word the program knows, then the string is a correctly spelled word.
- If there are no exact matches, generate all strings that are one change away from the test string.
- If any of them are words the program knows, choose the one with the greatest frequency in the overall corpus.
- If there are no exact matches or matches at an edit distance of 1, check all strings that are two changes away from the test string.
- If any of them are words the program knows, choose the one with the greatest frequency in the overall corpus.
- If there are still no matches, return the test string—there is nothing similar in the corpus, so the program can’t figure it out.
The point in the program that generates all the strings that are one change away is given below. This is the next place where you’ll need to edit the code to adapt it for another language!
def edits1(word):
# "All edits that are one edit away from `word`."
letters = 'abcdefghijklmnopqrstuvwxyz'
splits = [(word[:i], word[i:]) for i in range(len(word) + 1)]
deletes = [L + R[1:] for L, R in splits if R]
transposes = [L + R[1] + R[0] + R[2:] for L, R in splits if len(R)>1]
replaces = [L + c + R[1:] for L, R in splits if R for c in letters]
inserts = [L + c + R for L, R in splits for c in letters]
return set(deletes + transposes + replaces + inserts)Without getting into the technical details of the implementation, the code takes an input string and returns a set containing all strings that differ from the input in only one way: with a deletion, transposition, replacement, or insertion. So, if our input was ‘paer’, edits1 would return a set including (among other thing) par, paper, pare, and pier.
The code I’ve represented above will need to be edited to be used with many non-English languages. Can you see why? The program relies on a list of letters in order to create replaces and inserts. Of course, Estonian does not have the same alphabet as English! So for Estonian, you have to change the line that sets the value for letters to match the Estonian alphabet (adding ä, ö, õ, ü, š, ž; subtracting c, q, w, x, y):
letters = 'aäbdefghijklmnoöõprsštuüvzž'Once you make that change, it should be up and running! Before wrapping up this post, I want to discuss one key difference between English and Estonian that can lead to some different results.
A difference between English and Estonian: morphology!
In Norvig’s original implementation for English, a corpus of 1,115,504 words yielded 32,192 unique words. I chopped my corpus down to the same length, and I found a much larger number of unique words: 170,420! What’s going on here? Does Estonian just have a much richer vocabulary than English? I’d say that’s unlikely; rather, this has to do with what the program treats as a word. As far as the program is concerned, be, am, is, are, were, was, being, been are all different words, because they’re different sequences of characters. When the program counts unique words, it will count each form of be as a unique word. There is a long-standing joke in linguistics that we can’t define what a word is, but many speakers have the intuition is and am are not “different words”: they’re different forms of the same word.
The problem is compounded in Estonian, which has very rich morphology. The verb be in English has 8 different forms, which is high for English. Most verbs in English have just 4 or 5. In Estonian, most verbs have over 30 forms. In fact, it’s similar for nouns, which all have 12-14 “unique” forms (times two if they can be pluralized). Because this simple spelling corrector defines word as roughly “a unique string of letters with spaces on either side”, it will treat all forms of olema ‘be’ as different words.
Why might this matter? Well, this program uses probability to recommend the most likely correction for any misspelled words: choose the word (i) with the fewest changes that (ii) is most common in the corpus. Because of how the program defines “word”, the resulting probabilities are not about words on a higher level, they’re about strings, e.g., How frequent is the string ‘is’ in the corpus? As a result, it’s possible that a misspelling of a common word could get beaten by a less common word (if, for example, it’s a particularly rare form of the common word). This problem could be avoided by calculating probabilities on a version of the corpus that has been stemmed, but in truth, the real answer is probably to just build a more sophisticated spelling corrector!
Spelling correction: mostly an English problem anyway
Ultimately, designing spelling correction systems based on English might lead them to have an English bias, i.e., to not necessarily work as effectively on other languages. But that’s probably fine, because spelling is primarily an English problem anyway. When something is this easy to put together, you may want to do it just for fun, and you’ll get to practice some things—in this case, building a data set—along the way.